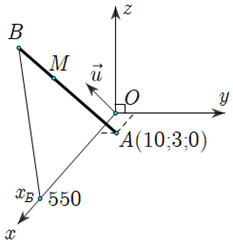
Một cabin cáp treo xuất phát từ điểm $A(10 ; 3 ; 0)$ và chuyển động đều theo đường cáp có véctơ chỉ phương là $\vec{u}=(2 ;-2 ; 1)$ với tốc độ là $4,5(\mathrm{~m} / \mathrm{s})$ (đ̛on vị trên mỗi truc tọa ảộ là mét) được mô hình hóa như các hình vẽ sau:

a) Phương trình chính tắc của đường cáp là $\frac{x-10}{2}=\frac{y-3}{-2}=\frac{z}{1}$.
b) Giả sử sau $t$ giây kể từ lúc xuất phát $(t \geq 0)$, cabin đến vị trí điểm $M$. Khi đó tọa độ của điểm $M$ là $\left(3 t+10 ;-3 t+3 ; \frac{3 t}{2}\right)$.
c) Cabin dìnng ở điểm $B$ có hoành độ $x_B=550$. Quãng đường $A B$ có độ dài bằng $810(\mathrm{~m})$ (làm tròn kêt quả đến hàng đàon vị của mét).
d) Đường cáp $A B$ tạo với mặt ( $O x y)$ một góc $22^{\circ}$ (làm tròn đến hàng đơn vị của độ).

Một bể cá đầy nước có dạng hình hộp chữ nhật $A B C D . E F G H$ với $A B=6(\mathrm{dm})$, $A D=8(\mathrm{dm})$ và cạnh bên bằng $10(\mathrm{dm})$. Một chú cá con bơi theo những đoạn thẳng từ điểm $G$ đến chạm mặt đáy của hồ, rồi từ điểm đó boi đến vị trí điểm $M$ là trung điểm của $A F$ được mô hình hóa như hình vẽ sau:

Để đường đi ngắn nhất thì chú cá boi đến điểm đưới đáy hồ cách $B A$ và $B C$ những đoạn bằng $a$ và $b$. Khi đó tổng $\mathscr{D}=3 a+6 b$ bao nhiêu ?

Xác suất để công ty $X$ thuê một trong hai công ty vệ tinh $A$ và $B$ tư vấn lần lượt là 0,4 và 0,6 . Theo kinh nghiệm khả năng $X$ phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn của công ty $A$ và $B$ lần lượt là 0,05 và 0,03 .
a) Xác suất để $X$ có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn là 0,038 .
b) Biết $X$ có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn. Xác suất để $X$ thuê công ty $A$ tư vấn là 0,4737 .
c) Biết $X$ có phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn. Xác suất để $X$ thuê công ty $B$ tư vấn là 0,5263 .
d) Biết $X$ không phát sinh thêm chi phí khi sử dụng dịch vụ tư vấn. Xác suất để $X$ thuê công ty $A$ tư vấn là 0,395 .

Một đoàn tàu đang đứng yên trong sân ga, ngay trước đầu tàu có một cái cây. Đoàn tàu khởi hành từ trạng thái đứng yên với gia tốc $a=0,005 t\left(\mathrm{~m} / \mathrm{s}^2\right)$ và đi qua cái cây trong thời gian 60 giây. Sau 80 giây đoàn tàu chuyển sang trạng thái chuyển động đều.

a) Vận tốc của đoàn tàu là $v=5 \times 10^{-8} t^2(\mathrm{~m} / \mathrm{s})$.
b) Chiều dài của đoàn tàu là $\ell=180(\mathrm{~m})$.
c) Sau 80 giây, đoàn tàu chuyển động với tốc tốc $57,6(\mathrm{~km} / \mathrm{h})$.
d) Sau khi chuyển động đều một thời gian, đoàn tàu gặp một cây cầu có chiều dài $480(\mathrm{~m})$. Khi đó đoàn tàu đi qua cây cầu đó trong thời gian 30 giây.

Cho hàm số $y=\frac{a x^2+b x+c}{m x+n}$ có đồ thị như hình vẽ sau:

a) Hàm số đã cho nghịch biến trên khoảng ( $-2 ; 0$ ).
b) Đồ thị của hàm số đã cho có tiệm cận xiên $y=x+1$.
c) Gọi $A, B$ là hai điểm cực trị của hàm số đã cho, diện tích của tam giác $O A B$ bằng 8 (với $O$ là gốc tọa độ).
d) Một trục đối xứng của đồ thị đã cho là $d: y=(x+1) \tan \frac{3 \pi}{8}$.